Analyse en Composantes Principales

1 - Notations
2 - Définitions
3 - Projections sur un sous-espace
4 - Axes principaux
5 - Facteurs principaux
6 - Composantes principales

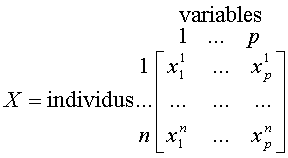
1 - Notations
– e1,. . ., en : vecteurs individus dans l’espace initial
– f1,. . ., fn : vecteurs individus dans l’espace de projection
– x1,. . ., xp : vecteurs variables
– p1,. . ., pn : poids associés à chaque individu
– g : centre de gravité du nuage de points dans l’espace initial
– Ig : inertie totale du nuage de points
Dans ce qui suit nous considérons que les variables sont centrées (la moyenne par colonne est égale à 0)

Les données que l'on doit traiter par l'ACP sont stockées dans un tableau X de type individus/variables de la forme suivante :

On a alors :

- p variables, représentées en colonnes
- n individus, représentés en lignes
- des valeurs prises par chaque variables, pour chaque individu, notées :

2 - Problèmes

Le problème est que si on analyse directement la matrice X, les résultats seraient faussés par les valeurs relatives des variables (Par exemple si les valeurs ont été mesurées dans des unités différentes). Préparer les données pour le traitement consiste donc à transformer le tableau de données pour réduire ces effets.
Une métrique est une matrice permettant de définir un produit scalaire et donc des distances entre individus ou entre variables. La métrique que l'on utilise de manière naturelle pour mesurer les proximités entre variables est celle définie par la matrice Dp qui est la métrique de la covariance quand les variables sont centrées :

Dp est diagonale et chacun des éléments de la diagonale est égal à 1/N .
Pour mesurer des distances entre individus, il n'y a pas de choix aussi naturel que Dp pour les variables et on prendra une matrice M, symétrique définie positive :

les métriques les plus couramment utilisées sont :

3 - Projections sur un sous-espace

L'ACP consiste à projeter les points sur une droite, un plan...un sous-espace à s dimensions (avec s < p) choisi de façon à optimiser un certain critère. Intuitivement, on cherchera le sous-espace donnant la meilleure visualisation possible de notre nuage de points. Un bon choix consiste à rechercher la plus grande dispersion (le plus grand étalement) possible des projections dans le sousespace choisi. On est amené ainsi à chercher une rotation de notre système d'axes initial (les variables) permettant de mieux voir notre nuage. Définissons u1 le vecteur unitaire (i.e. de norme 1; u1'u1=1) recherché; c'est le vecteur présentant la plus grande dispersion des projections.
On va chercher un sous-espace de l'espace initial tel que :

Il est donc clair ici que trouver les valeurs de fi les plus proches de celles de ei dans un nouvel espace, revient àmaximiser la dispersion (ou inertie totale) des fi.
L'inertie totale est définie comme la somme des distances de chaque individu au centre de gravité g. Dans l'espace initial, on a donc :

puisque g = 0 (les variables sont centrèes). En utilisant l'écriture matricielle, on montre facilement que :

où P est la matrice permettant de projeter le nuage de l'espace initial vers celui de l'espace des individus projetés.

4 - Axes principaux
Nous cherchons la droite maximisant l'inertie du nuage projeté sur cette droite. Soit
a, un vecteur de cette droite, on a :

Le but est donc de trouver a maximisant Tr(VMP).
On montre que a est le vecteur propre de la matrice VM associé à la plus grande valeur propre.
De manière plus générale, le sous-espace des projetés de dimension k est engendré par les k vecteurs propres de VM associés aux k plus grandes valeurs propres. On appelle axes principaux d'inertie les vecteurs propres de VM normés à 1. Il y en a p.

5 -Facteurs principaux

A l’axe principal a est associé le facteur principal u = Ma. En partant du fait que a est déterminé par le vecteur propre de MV correspondant, on montre que u est déterminé par les vecteurs propres de VM.

6 - Composantes principales
Ce sont les variables ci définies par les facteurs principaux :

ci = Xui

ci est le vecteur renfermant les coordonnées des projections des individus sur l'axe défini
par ai. Ce sont donc les combinaisons linéaires de x1,. . ., xp de variances maximales.
On montre que la variance de ci est égale à la valeur propre correspondante. Ces composantes sont orthogonales, et donc non corrélées entre elles.